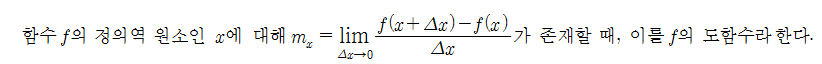미분

주의. 이 문서는 공머생들이 좋아하는 주제 혹은 공머생 그 자체에 대해 다룹니다. 본 문서가 다루는 내용에 지나치게 탐닉할 경우 필연적으로 여성들과 멀어지게 됩니다. 이는 디시위키가 책임지지 않습니다.

주의. 이 게임은 요령 없이 하다간 저절로 똥손, 똥발이 되어버리는 존나 어려운 게임입니다. 이 게임은 존나게 어려워서 몇 번이고 유다희 누님을 영접할 위험이 있습니다. 계속하면 정신이 나가 샷건을 칠 수 있으니 하기 전에 다량의 항암제를 준비하거나 전문가와 상의를 권고합니다. 하지만 이미 늦었군요, YOU DIED

개요

적분 거꾸로.

근데, 적분 거꾸로는 니가 머학을 안가면 쓸모가 없어서 버리게 될거고 머학을 갔다면 혼란스럽게하는 정의다.

쉽게 말하자면 어떤 변량의 변화율이다. 흔히 접하는 y=f(x) (정의역의 원소 x를 공역의 원소 y와 이어주는 함수 혹은 사상f )에 대하여 아주 미소한 변화 dx에 대한 변화량 dy 의 비율인 dy/dx를 구하는것을 미분한다고 한다. 뉴턴식 표기법으론 y', 라이프니츠식 표기법으론 dy/dx이다.

x=a에서의 f(x)의 순간변화율은 도함수에a대입하면 된다.

정의역이 벡터고 치역도 벡터인 함수는 미분하면 행렬이 나온다. 적분 거꾸로라는 생각은 급식충 지나면 버리는게 좋다.

다른 의미로는 함수를 함수로 선형변환하는 연산으로써 미분이 있다. 급식충때는 필요 없고 다변수 해석학이나 선형대수학 할 때 필요한 의미이다

미분! 적분! 이차함수!

米粉(쌀가루)

당신의 집안은 미분되었습니다!

당신의 집안은 미분되어 0이 되었습니다!

집에 e를 하나 장만해놓으면 집안이 미분되는 걸 방지할 수 있다.

ㄴ편미분하면 어쩔거냐

ㄴ전구간연속이고 전구간 미분 불가능한 바이어슈트라쓰 함수를 갖다 놓으면 된다.

ㄴ히이이익 미분귀신이다

널 미분하고 싶어~ 니가 0이 될때까지~ 너가 아무리 높은 고차함수 라도~....

진짜 개요

이 문서는 이해하기 어려운 대상을 다룹니다. 이 문서는 일반적인 뇌를 가지고도 이해하기 어려운 대상에 대해 다룹니다. 두뇌를 풀가동해도 아마 이해하기 어려울 것입니다.

이 문서는 아직 완성되지 않은 대상을 다룹니다. 이 문서는 미완성된 문서입니다. 하루빨리 완성시켜 주시기 바랍니다. 그리고 아직 이 대상은 완성이 못 되었기 때문에 평가하기에 이릅니다. 섣부른 판단과 수정은 금물입니다.

微分(작을 미, 나눌 분)/Differentiation

한 지점의 변화율을 알기 위해 쓰이는 개념이다. 미생물을 나눈다하더라. ㅋㅋㅋ 미분을 알기 위해서는 우선 몇 가지 개념들에 대한 이해가 필요하다.

변화율과 미분계수

변화율이란 어떤 변수들이 변화한 정도의 비이다. 예를 들어 함수 y=x²에서 x의 값이 1부터 3까지 변하면 yyy의 값은 1부터 9까지 변화한다. 이때 독립변수 x의 변화량은 2이며, 이를 x의 증분이라 하고 그리스 문자 Δ(델타, Delta)를 사용하여 Δx로 나타낸다. 델타덕후.

또, 종속변수 y의 변화량인 8을 Δx에 대한 y의 증분이라 하고, Δy로 나타낸다. 이때 y의 증분 Δy를 x의 증분 Δx로 나눈 를 닫힌 구간 [1,3]에서의 y의 평균변화율이라고 한다.

기본 공식 설명

“

”

이 정도는 개념정도로만 알아두고 미분 계산에서는 일일히 이 공식으로 유도하려면 머가리 깨지니까 급식충 수준에서는 공식을 외우도록

미분 가능성과 연속

이에 대한 증명: 어떤 함수가 x=c 에서 연속이라는 것은 이므로 이를 증명하면 된다.

이 정리의 역은 성립하지 않는다. 즉, f가 c에서 연속이면 f가 c에서 반드시 미분가능한 것은 아니다.

이 외에 미분 가능하지 않은 것들: 뾰족점 함수, 기울기가 발산

도함수

이 문서는 교묘하게 거짓을 말하고 있습니다. 이 문서의 내용은 얼핏 봐서는 진실인지 거짓인지 구별하기 힘들 정도로 정교한 거짓말로 가득 차 있습니다. 만약 이 내용에 낚여서 피해를 보게 될 경우 원 작성자를 굴다리로 불러내서 존내 패버릴 것을 추천합니다. "이 새끼가 어디서 약을 팔아?"

이 문서는 특정 분야에서 도를 닦고 깨달음을 얻으신 분에 대해 다룹니다. 이 분야에서 이분만큼이나 도를 닦고 수련하여 통달하신 분은 거의 없습니다. 이분의 말씀은 진리이자 불변의 법칙과도 같습니다. 디시위키 이용자들은 이분의 말씀에 반박하는 것에 대해 다시 한 번 생각해 주십시오.

위에서 정의한 미분계수를 일반화시킨 개념으로 도를 닦고 깨달은 함수라 한다. 그러니 밑의 정의를 보자.

도함수의 흔한 공식

(xⁿ)'=nx^n-1

왜 이렇게 나오는 이유는 위의 정의들을 이용해라. 머가리 터지겠지만...

참고로 위같은 식을 보고 뭐야.. 미분 좆밥이네 하다가 통수 맞을 수 있으니 얕보면 안된다.